
En nuestro texto “Optimiza 3 – Modelos, simulación y teoría de la decisión”, hemos abordado, directa o indirectamente, el concepto Entropía al menos en tres oportunidades: en el Capítulo 1, al mencionar “la tendencia al desgaste de los sistemas”; en el Capítulo 4, al mencionar los requisitos que debe cumplir un generador de números aleatorios, donde mencionamos el blanqueamiento de Von Neuman o destilación de entropía, como método que ofrece “seguridad de Shanon” y también en el Capítulo 1, destinado a Teoría de la Información, donde hablamos nuevamente de Claude Shannon, aunque no directamente de entropía, pero sí de su teoría matemática de la información que tiene uno de sus pilares en ella.
Debemos señalar que la entropía es un concepto muy particular que se utiliza en el campo de la física, específicamente en termodinámica, en la parametrización de los contenidos de energía de un sistema, y que tiene la particularidad de que no es una magnitud ni una ley física. Lo que la hace especial, además, es que no se cumple estrictamente, ni aun en sus propios ámbitos. Esto se debe a que se trata de un concepto estadístico referido a los comportamientos macroscópicos de la materia o de la energía en base a los estados microscópicos (microestados) de ese estado (macroestado). Esto implica que solo se puedan abordar esos comportamientos en términos estadísticos.Si bien el párrafo anterior puede ser un galimatías y aún cuestionable, y pidiendo permiso a los termodinámicos y a los físicos, vamos a tratar de explicar algo de lo que concierne a nuestros temas desde un punto de vista muy simplificado con el objetivo meramente informativo y sin pretender presentarlo como un tratado sobre la entropía.
Debemos recordar que hemos oído conceptos muy arraigados. como por ejemplo:
“la entropía de los sistemas tiende naturalmente a aumentar a medida que transcurre el tiempo”
y que solemos recurrir a casos de la naturaleza para demostrar que esto es cierto: por ejemplo, sabemos que una copa de vidrio (estado cuyos componentes están ordenados) que se rompe (estado cuyos componentes están desordenados) nunca se recompone espontáneamente y vuelve a ser una copa aunque pase mucho tiempo. Llamamos a esto “proceso irreversible” y es una de las bases del segundo principio de la termodinámica cuando se aplica a fenómenos que implican el uso, el aprovechamiento o la simple disipación de la energía.
En el capítulo 1 de este libro, nos referimos a las propiedades de los sistemas y, entre ellas mencionamos a la entropía con la siguiente definición:
Entropía: que es la tendencia de los sistemas a desgastarse, a desintegrarse, relajar los estándares y aumentar la aleatoriedad. La entropía aumenta con el tiempo. Si aumenta la información, disminuye la entropía, porque es la base de la configuración y del orden. Obviamente el proceso entrópico, en tanto se trata de un proceso termodinámico, implica que hay un consumo irreversible de energía e información para mantener la integridad del sistema.
En esta definición estamos relacionando claramente varios conceptos fundamentales: información, energía, orden, aleatoriedad y tiempo.
Por experiencia sabemos que hay comportamientos de la materia que son irreversibles, es decir que no tienen una simetría “natural” a menos que se use energía externa. El ejemplo clásico es el de un recipiente lleno de agua, separada en dos cavidades por una compuerta: el agua de la izquierda tiene disuelta cierta cantidad de tinta y la derecha está pura. Así tenemos agua azul a la izquierda y clara a la derecha. Si sacamos o abrimos la compuerta, vemos que, al cabo de un tiempo, el agua se mezcla (el agua con colorante se difunde en todo el recipiente) y tenemos el recipiente completo con agua coloreada. Por más que dejemos pasar tiempo, lo contrario no ocurre: no queda el lado izquierdo con agua azul y el derecho con agua clara o viceversa, aunque pongamos nuevamente el tabique o aunque esperemos mucho tiempo. (Fig. 1)
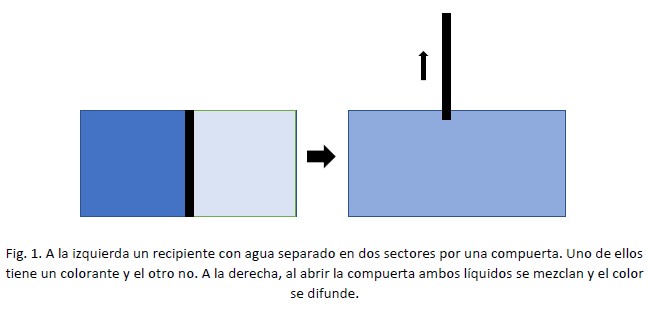
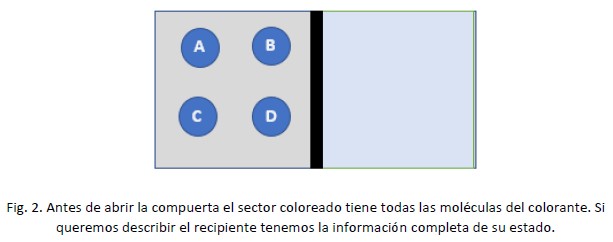
Ahora vamos a suponer que en el lado “azul”, con la compuerta puesta en su lugar, solo tenemos 4 moléculas de colorante, y que las tenemos perfectamente identificadas: son las moléculas “A”, “B”, “C” y “D”. (Fig. 2)
Acá podemos notar algunas cosas interesantes. La primera es que tenemos toda la información posible sobre el estado del sistema “agua con color” sabemos dónde están todas y cada una de las moléculas del colorante (en el lado izquierdo) y donde NO están (en el lado derecho). Además sabemos que, en estas condiciones, no hay otra posibilidad.
Ahora vamos a abrir la compuerta y vemos que tenemos cuatro posibles estados:
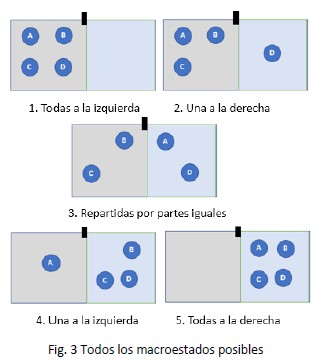
- Que solamente una de ellas pase a la derecha y las otras tres queden a la izquierda
- Que la mitad de ellas pasen a un lado y la otra mitad no pase
- Que tres pasen a la derecha y una permanezca en la izquierda
- Que las cuatro pasen a la derecha.
Podemos decir que cada uno de estos estados es un “estado no específico” o macroestado. Tenemos, entonces, cinco macroestados para el caso de un recipiente que originalmente tenía dos cavidades y cuatro moléculas.
En el primer estado, tenemos información completa sobre la situación de cada molécula. Cada una de las cuatro está en el mismo sector. No hay otra posibilidad. Esto puede ocurrir entonces en un solo y único caso (o microestado) sobre los cinco posibles.
No es así el segundo caso, una a la derecha y tres a la izquierda, porque acá tendremos estas posibilidades:
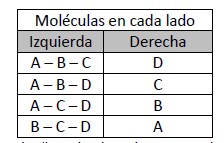
Como vemos para el macroestado “1 a la derecha, tres a la izquierda” hay cuatro estados particulares posibles (microestados) y tenemos que admitir que debemos buscar información extra para saber en cuál de esos microstados estamos. Hemos perdido información respecto al caso anterior. También sabemos que cada “microestado” tiene la misma probabilidad.
Para el tercer caso, “2 a la derecha, 2 a la izquierda”, tenemos seis posibles escenarios:
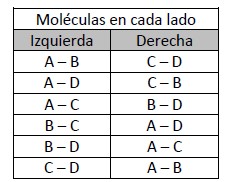
Como vemos ahora hay seis microestados posibles con la misma probabilidad y tenemos que averiguar, conseguir información, sobre que moléculas están a la derecha, ya que puede haber una sola combinación de seis posibles. Hemos perdido aún más información.
Obviamente si analizamos lo que ocurriría con tres moléculas pasando a la derecha tendríamos el mismo razonamiento que en caso 2. Y si estuvieran todas a la derecha sería lo mismo que el punto de partida.
Podríamos hacer un gráfico de estados posibles (microestados) para cada uno de los estados inespecíficos. Los microestados posibles están en el eje de la “y” y los macroestados en el de las “x”
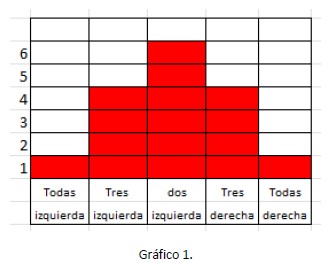
Nos encontramos con que hay 16 microestados posibles y que solo nos encontraremos en el macroestado “todas a la izquierda” una vez cada 16 estados que se den (1/16) y 1/16 (0,065) veces que estén “todas a la derecha”. Esos dos serían casos de “máximo orden posible”, aunque son posibles, tenemos pocas chances de que ocurran.
Los casos con un desorden un poco mayor podrán darse con algunas posibilidades más, porque van a aparecer 4 veces entre 16 posibles, que es 4/16 = 0,25, pero el caso de máximo desorden lo vamos a encontrar 6 veces entre 16 posibles (6/16 = 0,375).
Si hacemos la suma de estos números, tenemos
Todos izquierda + una a la derecha + dos a la derecha + tres a la derecha. + todos a la derecha
(1/16) + (4/16) + (6/16) + (4/16) + (1/16) = (1 + 4 + 6 + 4 + 1) / 16 = 16/16
Esta suma nos dice que forzosamente debemos estar en uno de estos 16 casos. Además podemos decir que estamos calculando las probabilidades de encontrarnos en un estado determinado y que solamente nos encontraremos en uno de ellos porque al ser la suma igual a uno, las probabilidades son excluyentes.
La pregunta es, ¿El sistema evoluciona por alguna ley de la naturaleza al máximo desorden? La respuesta es No. Ocurre algo mucho más simple: es más probable encontrar al sistema en un estado donde existan muchas más combinaciones de microestados que en cualquier otro que tenga menos combinaciones. Simplemente, al haber más microestados en un macroestado, es más probable caer en uno que en el que en otro.
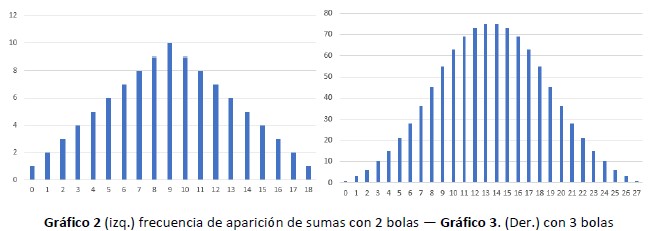
Si además pensamos que el colorante no tiene cuatro, sino miles de millones de moléculas, veremos que las probabilidades de encontrar un sistema ordenado son absolutamente despreciables porque se demuestra que, a medida que aumentamos el número de componentes la distribución de estados posibles centrada en el caso más frecuente (Gráfico 1) se hace cada vez más estrecha[1].
[1] Un ejemplo claro que se usa habitualmente es con dados: si se usa un dado la probabilidad de encontrar cualquier cara es la misma para las 6 caras. Si se usan dos dados, la probabilidad de encontrar la suma de caras vemos un mínimo de frecuencias para la suma 2 o la suma 12 que solo se pueden conseguir si ambos dados tienen un as o ambos un 6. La máxima frecuencia aparece con la suma 7, que se puede conseguir con 6 combinaciones de ambos dados: 1-6, 2-5, 3-4, 4-3, 5-2 y 6-1. Es claro que si usamos 1000 dados, nadie esperaría encontrar el número 1000 o el 6000, ya que eso solo se podría lograr si los 1000 dados cayeran simultáneamente en 1 o en 6, aunque la probabilidad existe, en términos prácticos es casi cero. [(1/6) elevado a la 1000]. Si en vez de dados sumamos los números de dos bolas numeradas del 0 al 9, tendremos una distribución como la del gráfico 2. Y de tres bolas también del 0 al 9, como la del gráfico 3. Ahí comprobamos como se estrecha la curva de frecuencias.
Lo mismo ocurrió con la información: a medida que hay posibilidades de encontrar las moléculas distribuidas en cualquier orden, vamos perdiendo información sobre el lugar donde encontraremos una molécula en particular.
En el caso 1 y 5, el sistema tiene el máximo orden posible y solamente tenemos 1 grado de libertad en 16 opciones para describir exactamente el sistema y saber en qué recinto está cada una de las moléculas. Menos ordenado, casos 2 y 4, ahora tenemos cuatro combinaciones diferentes para cada recinto de posibles situaciones de cada molécula. Totalmente desordenado, ahora tenemos 6 posibles combinaciones de estados posibles para cada una de las moléculas, hemos perdido aún más información.
La PRIMERA CONCLUSIÓN de estas líneas es que la entropía no es una propiedad intrínseca de la materia o de la física o de la termodinámica o de la información. Es un principio estadístico.[1]
La SEGUNDA CONCLUSIÓN es que podemos definir la entropía exclusivamente como un fenómeno estadístico si usamos la expresión siguiente:
S = k ln X,
Siendo S entropía, k la constante de Boltzman, y X la cantidad de microestados posibles equiprobables. Debemos prestar atención a este término: equiprobables. Por ejemplo una molécula a la derecha/tres a la izquierda es un estado válido si la probabilidad de que la molécula sea la “A” es la misma que la probabilidad de que sea la “B”, la “C” o la “D”.
[1] A pesar de esta afirmación debemos recordar que las interacciones entre las partículas reales existen y contribuyen a que aumente la entropía termodinámica. Este ejemplo es simplificador.
Por ejemplo, si tenemos que calcular la entropía de una moneda (bit), que tiene solo dos estados, cara o ceca, nos quedaría, S = k ln 2. Podemos asimilar X a la información disponible.
De nuevo, en la moneda, esa información es cara (0) y ceca (1). En el caso de nuestras 4
moléculas tendremos S = k ln 24, lo que da que S es proporcional a 16… ya que 2 es el número de estados posibles (derecha o izquierda) y 4 es el número de componentes totales.
La TERCER CONCLUSIÓN es que la entropía está relacionada con la pérdida de información. A medida que aumenta la entropía, hemos visto, aumenta la pérdida de información. Aumenta la incertidumbre. Aumenta la aleatoriedad.
Basado en estos conceptos (que acá hemos simplificado al máximo posible) es que se trabaja en base a entropía de sistemas para diseñar generadores pseudoaleatorios criptográficamente seguros.
El concepto es obtener secuencias de bits mediante un generador binario que soporte la llamada “prueba del siguiente bit”: Dados los primeros k bits de una secuencia aleatoria, no debería haber ningún algoritmo que pueda predecir el bit k+1 con una probabilidad de éxito superior a
0,5.
Veamos esto en términos de entropía. Como se trata de bits binarios, podemos usar S = k log2 X.
Si graficamos en las x la probabilidad de cada uno de los estados posibles de ocurrencia de un bit aleatorio (0 o 1, o cara y ceca) y en ordenadas la medida de entropía, llamando 1 a la entropía de la máxima probabilidad de ocurrencia del bit, tenemos que para una probabilidad de 0,5 habrá una entropía máxima de 1. (log2 2 = 1)
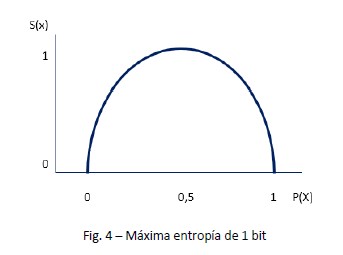
von Neumann probó que un algoritmo simple puede eliminar cualquier sesgo de un flujo de bits (a este proceso se lo conoce como destilación de entropía o blanqueamiento) si se aplica en conjunto con un procedimiento de generación de una serie aleatoria.
Veamos como ejemplo una secuencia de 1 bit, (digamos que genera una secuencia en que cada bit es k.) Le agregamos como parte de la destilación un bit “de blanqueo” que genera la secuencia k+1, vamos a obtener dos bits con cuatro posibles combinaciones: 00 – 01 – 10 – 11. El blanqueamiento de von Neuman nos entregaría al final un solo bit proveniente de desechar de estos cuatro los casos 00 y 11 porque presupone que en ellos el segundo bit fue “anunciado” por el primero y nos dejaría solamente con las combinaciones 01 y 10, los que se presentarían, como dijimos, como un solo bit: para 01 obtendríamos 0 y para 10 un 1.
Hemos obtenido un bit de entropía máxima usando un bit para blanquearlo.
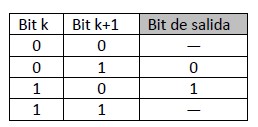
Si la entropía es función de la probabilidad de que X sea igual a 1, cuando la probabilidad P(X=1) sea 0,5 entonces todos los resultados posibles son equiprobables. Máxima entropía, máxima impredecibilidad. Es la prueba de la moneda. Si un proceso tiene la misma impredecibilidad que tirar una moneda, entonces es verdaderamente aleatorio.
De esta manera, la mención que hemos hecho a la teoría de comunicación en el capítulo 1, cuando la describimos como una aplicación de la TGS, encierra un grado de complejidad ya que la propuesta de Claude Shannon tiene como punto principal la entropía. En este caso se trata de una magnitud física (información) que es una secuencia de caracteres cuyo nivel de información se puede medir con la entropía y el mensaje en términos de cadena cuya información se mide con una secuencia de bits.
El principio es el siguiente: supongamos el caso de un mensaje. La probabilidad de acceder al contenido de cada mensaje no es igual para todos los mensajes. Sabiendo esto el emisor va a “gastar” más bits en codificar los mensajes menos probables y menos en los más probables. Por ejemplo si el mensaje es “hay que medir 10 centímetros”, es muy probable que si se emite el solamente “medir 10 c” el receptor “entienda” (no pierda información) que la c se refiere a “centímetros” y no note la ausencia de “hay que” ya que aporta mucho menos información que el resto. Dicho de otra manera no parece que sea necesario mandar el mensaje completo. El contexto referido a medida (en infinitivo) y la unidad que comienza con c son suficientes. Por el contrario, si el mensaje original fuera “hay que adquirir 10 computadoras” y nos limitamos a mandar el mensaje “adquirir 10 c” seguramente necesitamos más información, porque si bien es cierto que hay que sigue siendo de baja importancia, en este contexto el carácter “c” perdió información porque puede ser interpretado como “computadora”, “carcaza”, “conector”, “cable”, etc. Debemos aumentar la longitud del mensaje porque la información alta que había en el carácter “c” del primer mensaje se perdió en el segundo caso.
Por esto se usa para todos los mensajes emitidos por una fuente un promedio ponderado de la longitud del código que se calcula en función de las probabilidades de ocurrencia de dicha longitud. Este promedio es la entropía de la fuente y sirve para cosas tan cotidianas como, por ejemplo, comprimir un archivo para enviarlo por correo electrónico. Se demuestra que la entropía de una fuente depende de la probabilidad de cada carácter emitido. (por ejemplo, en español, la “a” es más frecuente que la “w” en cualquier conjunto, por tanto “w” transmite más información que “a”).
En contexto de un mensaje, no cambia mucho la información si se transmite “iremos al cine” como “iremos cine”. En este caso, la partícula omitida (“al”) posee muy poca información. En cambio si hemos transmitido solamente “iremos al” hemos perdido mucha información al omitir la partícula “cine”
Es común que para medir la información se ejemplifique con la cantidad de mensajes que serían necesarios para responder la supuesta pregunta que originó estos mensajes. Muchas veces la respuesta es binaria (SI – NO) y con 1 solo bit alcanza para responder una pregunta simple
(¿estás en viaje?). Pero no así para otras preguntas (¿En qué fecha te queda bien reunirnos en Rosario?) Esta definición llevó a Shannon a imaginar que, sin importar lo compleja que sea la pregunta, la misma pregunta se podía desglosar en una cantidad de preguntas simples que nos llevaría a la respuesta.
Veamos un ejemplo: Queremos saber quién produjo un informe de entre los miembros de un equipo formado por dos hombres y dos mujeres, cuyos nombres son Juan, Pedro, Ana y Belén. Como la pregunta ¿Quién escribió el informe? No nos sirve porque no hay respuestas por SI o por NO, vamos a averiguarlo mediante preguntas de respuestas binaria:
- El que escribió el informe, es hombre?, La respuesta por SI o por NO elimina al 50% de los candidatos.
- La segunda pregunta, en función de la respuesta a la primera sería: Su nombre comienza con J? (si era hombre) Su nombre comienza con A? (si era mujer). Con esta segunda respuesta tenemos el nombre preciso. Hemos necesitado solamente 2 bits para reconstruir un mensaje con 4 posibles respuestas.
De esta manera vemos que dividiendo la cantidad de opciones en grupos con algún criterio podemos elegir cualquier cantidad de opciones y dividirlas sucesivamente por la mitad hasta llegar a una única alternativa. Para saber cuántas veces vamos a dividir una cantidad por 2 para llegar a la unidad usamos nuevamente el logaritmo en base 2 del número de preguntas.
𝐻 = 𝑙𝑜𝑔2 𝑥
En este caso el log2 de 4 es 2. Si el caso fuera saber mi PIN de acceso a Window, que es un número de 5 dígitos, tendría que responder log2 de 100.000 = 16,6 preguntas o 16 bits para acceder al número correcto. Quizá en este punto se entiende un poco mejor la destilación de entropía de von Neumann que mencionamos un poco más arriba.
Sin embargo este ejemplo supone que la mitad es masculina y la mitad es femenina. Pero, no siempre esto es posible, por ejemplo, ¿Qué ocurre si sabemos de antemano que solo puede haber un hombre y dos mujeres?
Digamos que son Juan, Ana, Belén y Beatriz. Ahora necesitaríamos hacer estas preguntas, que se responden por SI o por NO:
- Es Mujer? (si la respuesta es NO ya conocemos el mensaje y hemos usado un solo bit)
- Si la respuesta es SI: ¿su nombre comienza con “B”? (si la respuesta es NO ya sabemos que es Ana y hemos gastado 2 bits)
- Si la respuesta es SI: ¿Su nombre finaliza con “z”? y obtenemos la respuesta gastando 3 bits
Hemos necesitado 1 bit en un camino, 2 en el segundo y 3 en el tercero.
En estos casos la primera respuesta condiciona la(s) siguiente(s) pregunta(s) y cambia el estado en antes de la pregunta y después.
Si en lugar de usar el log2 de la cantidad x de estados, ahora probamos con la expresión

Tendremos para el primer ejemplo, (cuando había 2 hombres y 2 mujeres): SI (es hombre)
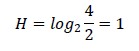
Segunda pregunta, tanto como si la primera respuesta fue SI como si fue NO)
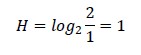
Como vemos, el número de bits es igual al que encontramos anteriormente con el otro método.
En el segundo ejemplo (un solo hombre) las preguntas no dividen por la mitad. La primera es para el saber si es hombre o no:
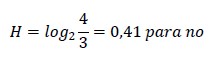
Quiere decir que ahora esta pregunta tiene menos información que antes, ya que “vale” 0,4 bits (o sea, esta sola vale casi como media pregunta de las de antes o como dos preguntas si fue contestada como si), para saber, con una sola que se trata de un hombre. Así que resulta práctico ordenar las preguntas según la importancia que tienen en el mensaje. Sabemos que 1 de cada cuatro personas es Hombre, pero que 3 de cada 4 es mujer. Tendremos 2 opciones antes de preguntar y solo 1 después de hacerlo.
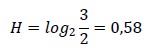
Que significa que esta respuesta también tiene poca información (excepto que la respuesta sea SI), ya que seguimos dudando entre personas restantes, lo que nos lleva a hacer una tercera pregunta, que, al ser la última, siempre valdrá un bit:
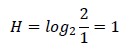
Fuimos pasando de 4 personas a 3, de 3 a 2 y de 2 a 1.
Esta forma de ver el problema se relaciona con la probabilidad de que sea un hombre (1/4) o que sea una mujer (3/4) y aún en ese caso que su nombre comience con “B” (2/3) o con “A”. Por este motivo, como los números son los mismos pero inversos, la expresión de Shannon también la podemos escribir así pensando en hacer una media ponderada de respuesta que necesito según las preguntas:
𝐻 = 𝑙𝑜𝑔2 (1⁄𝑝)
¿Cómo se expresa esto como información? Si supiéramos la respuesta (p = 1) no necesitamos información. Si tenemos un 50% de probabilidad de saber la respuesta, (p = 0,5) tenemos 1 bit de información, y si, en cambio, la probabilidad de conocer la respuesta tiende a cero, más bits de información necesitamos y obtenemos de ella.
Finalmente, como estamos usando probabilidades que pueden ser diferentes en cada uno de los pasos, lo que haremos es usar una media ponderada para calcular la cantidad final de entropía del mensaje:
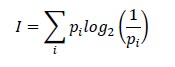
En el ejemplo de 1 hombre y 3 mujeres, tenemos una probabilidad de 0,25 para hombre y de 0,75 para mujer, por lo tanto, necesitaremos 0,8 bits promedio ponderado para llegar a la
respuesta.
En la Figura 5 comprobamos que para llegar a Juan necesitamos 1 bit, para Ana 2 bits y para el resto (Beatriz o Belén), 3 bits.
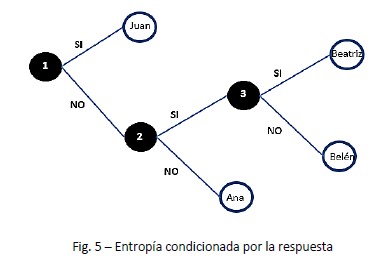
La probabilidad de que sea Juan es de ¼, podemos escribir
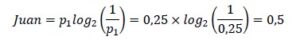
Nos queda un remanente de 3 personas. El factor ponderado de que sea Ana será
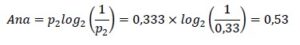
𝑝2 0,33
Ahora solo nos quedan 2 personas, cada una de ellas tiene la misma probabilidad y su factor de ponderación será
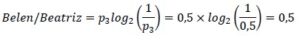
Entonces, la cantidad media de bits necesarios será
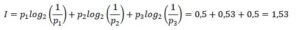
Que significa que llegamos a la pregunta final con menos de 2 bits.
Obviamente, este es un ejemplo pueril, aunque sigue siendo válido es situaciones más complejas.
Fuentes:
John von Neumann, 1963, “Various techniques for use in connection with random digits” . The Collected Works of John von Neumann. Pergamon Press, pp. 768-770 ISBN 0- 8-009566-6
McKay, David, 2003. “Information Theory, Inference and Learning Algorithms”, Cambridge University Press.
